تعد المضلعات من الأشكال الهندسية المهمة في علم الرياضيات، إذ تستخدم في العديد من التطبيقات الهندسية والعلمية، ومن بين هذه الأشكال توجد أنواع مميزة تعرف بالمضلعات المتشابهة والمتطابقة، ولكل منها خصائص تميزها عن الأخرى وتساعد في فهم العلاقات الهندسية بين الأشكال.
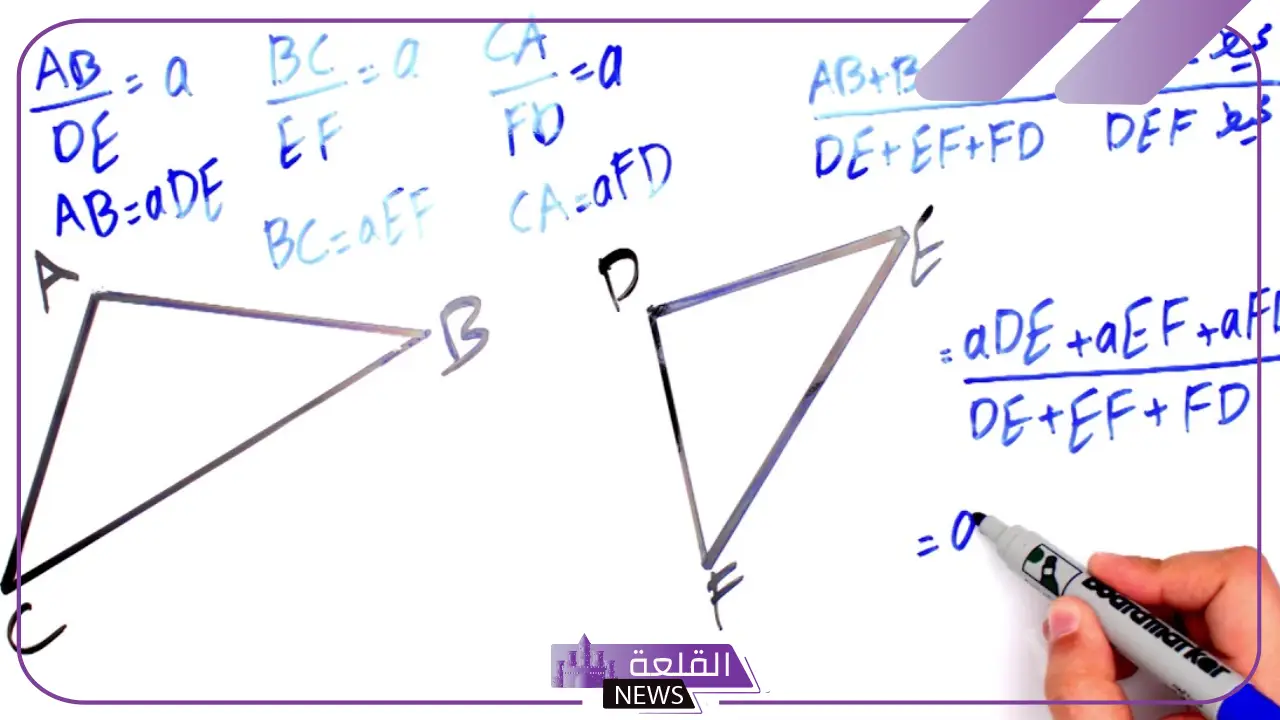
تسمى المضلعات التي لها نفس الشكل والقياس المضلعات المتشابهة
- المضلعات المتشابهة هي تلك التي تتشابه في الشكل العام لكن على الرغم من اختلاف حجمها.
- ويكون التشابه بين أضلاعها متناسب وزواياها متطابقة، مما يجعلها متساوية في النسبة دون أن تكون متطابقة تمامًا.
- يستخدم مفهوم التشابه في مجالات مثل رسم الخرائط والنماذج المصغرة، إذ يسمح بتمثيل الأشكال الكبيرة بصورة دقيقة ومتناسبة.
- من أهم خصائص التشابه أن الزوايا بين الأضلاع تبقى كما هي في حين تتغير الأطوال بنسبة محددة، مما يجعل التشابه أداة أساسية في دراسة النسب الهندسية والمقاييس.
- التشابه في المضلعات يعد وسيلة لفهم النسب بين الأشكال في الحياة الواقعية مثل تصميم المباني والجسور والأعمال الفنية المعمارية التي تعتمد على التناسق الجمالي.
اقرأ أيضًا: ملخص درس متباينة المثلث
تسمى المضلعات التي لها نفس القياس والشكل المضلعات المتطابقة
- المضلعات المتطابقة تتشابه في الشكل والحجم معًا، أي أن أطوال الأضلاع متساوية والزوايا متطابقة تمامًا، مما يجعل الشكلين نسخة مطابقة لبعضهما.
- هذا التطابق يستخدم في التحقق من دقة الرسومات الهندسية أو في تصميم القطع المتوافقة في الهندسة الميكانيكية والعمارة.
- في المضلعات المتطابقة يمكن وضع أحد الشكلين فوق الآخر تمامًا دون وجود أي اختلاف، وهو ما يميزها عن المضلعات المتشابهة التي تختلف في الحجم فقط.
- التطابق يساعد الطلاب والمهندسين على إدراك مفهوم التماثل الهندسي، وكيفية تطبيقه في الرسم والتحليل المكاني.
خصائص المضلغات المتشابهة
- تتناسب أطوال الأضلاع المتناظرة في المضلعات المتشابهة بنسبة ثابتة، ويُعرف هذا التناسب باسم “نسبة التشابه”.
- زوايا المضلعات المتشابهة تكون متطابقة في القياس رغم اختلاف مساحة الشكل الكلية، وهو ما يبرز أن التشابه يعتمد على النسب وليس على الأبعاد.
- يمكن من خلال خصائص التشابه حساب أطوال أو مساحات غير معروفة عند توفر شكل مشابه معلوم النسب، مما يجعلها أداة قوية في التحليل الهندسي.
- تستخدم خصائص المضلعات المتشابهة أيضًا في التصوير ثلاثي الأبعاد ونمذجة الأجسام، لأنها تحافظ على العلاقات النسبية بين الأبعاد رغم التغيير في الحجم.
فهم الفروق بين المضلعات المتشابهة والمتطابقة يعزز القدرة على تحليل الأشكال بدقة، ويساعد في تطبيق المفاهيم الرياضية في مجالات التصميم والهندسة كما يسهم في بناء الإدراك الهندسي السليم للطلاب.