تعتبر الإحداثيات القطبية واحدة من أشهر المفاهيم الأساسية في عالم الهندسة والرياضيات، حيث يتم استخدامها لوصف موقع النقاط بطريقة مختلفة عن الإحداثيات الديكارتية التقليدية، وتعتمد هذه الطريقة على الزاوية والمسافة بدلًا من الإحداثيات الرأسية والأفقية فقط، الأمر الذي يجعلها ملائمة أكثر في بعض التطبيقات العلمية والعملية.
فهرس بحث عن الاحداثيات القطبية
- مقدمة بحث الإحداثيات القطبية
- مفهوم الإحداثيات القطبية في الرياضيات
- استخدامات الإحداثيات القطبية في الحياة
- خاتمة بحث الإحداثيات القطبية
اقرأ أيضًا: بحث عن النحاس
مقدمة بحث الإحداثيات القطبية
تعد الإحداثيات القطبية من الأنظمة الهامة التي توفر طريقة مختلفة عن الإحداثيات الكارتزية، حيث تعتمد على قياسين رئيسيين وهما: البعد عن نقطة الأصل “القطب” والزاوية المحصورة بين الشعاع الواصل بين النقطة والقطب، وخط المرجع، وعادة تُستخدم تلك الطريقة بشكل أوسع في التطبيقات الهندسية والفيزيائية، نستعرض لكم خلال بحثنا الآتي مفهوم الإحداثيات القطبية واستخداماتها في الحياة وأهميتها.
مفهوم الإحداثيات القطبية في الرياضيات
- تٌعرف الإحداثيات القطبية بأنها نظام يتم استخدامه لتحديد موقع نقطة في مستوى ثنائي الأبعاد.
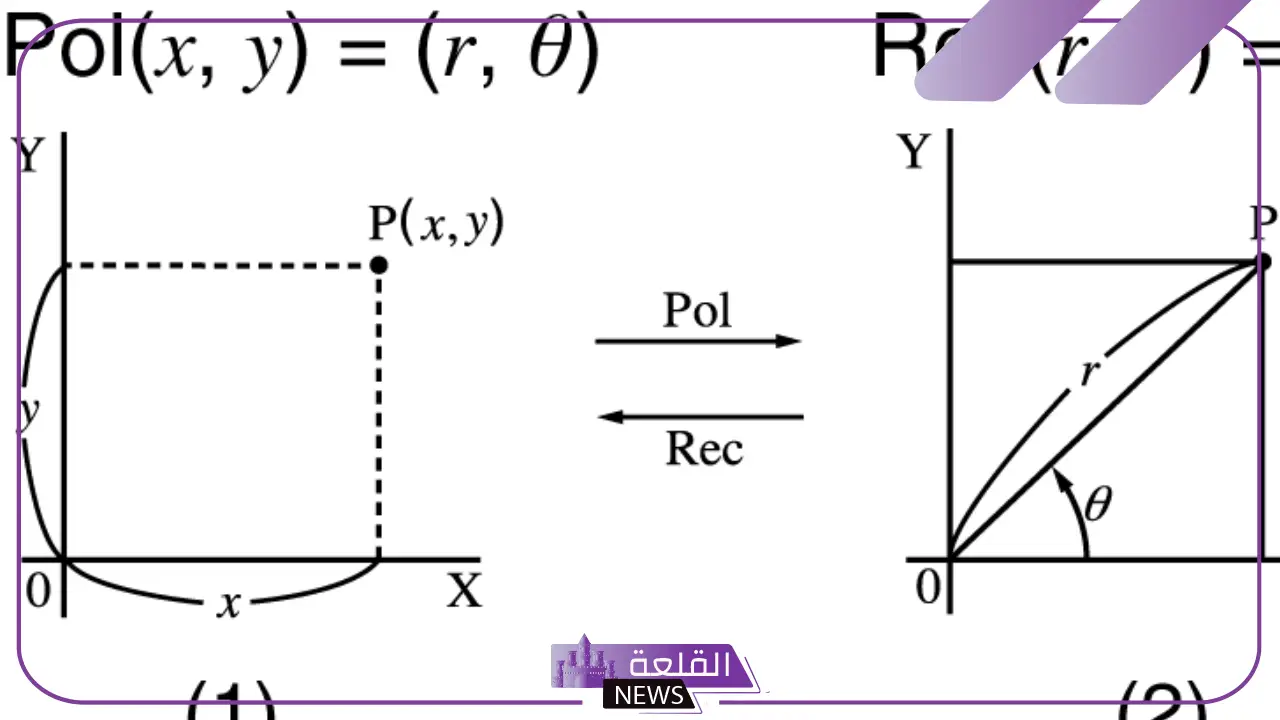
- يٌرمز إلى تلك الإحداثيات على الأغلب بالزوج (r, θ)، حيث أن r نصف القطب “أي المسافة من القطب” بينما θ الزاوية المقاسة بالراديان أو الدرجات.
- تعتبر تلك الطريقة فعّالة بشكل خاص في تحليل الحركات الدوّارة والدائرية.
- تسهّل من التعبير عن العلاقات الرياضية في أغلب المعادلات التي تتضمن دورات والمعادلات التفاضلية.
- من أبرز خصائص هذا النظام توفير مرونة في توصيف الدوائر والمسارات المنحنية، كذلك يمكن استخدامه بسهولة في المجالات الفيزيائية والهندسية، مثل تحليل دوائر التيار الكهربي وحركة الكواكب.
استخدامات الإحداثيات القطبية في الحياة
- الفلك والفيزياء مثل دراسة انتشار الموجات والمدارات.
- الخرائط والملاحة مثل الملاحة الجوية والبحرية.
- أجهزة تحديد المواقع والرادارات.
- الرؤية الحاسوبية لتحليل الأشكال الدائرية.
- الفن والتصوير للتصميمات المنحنية.
- نظم الملاحة في السيارات.
اقرأ أيضًا: بحث عن الإلكترونيات
خاتمة بحث الإحداثيات القطبية
تمثّل الإحداثيات القطبية أداة هامة في العلوم التطبيقية والرياضيات، حيث تسهم في تبسيط الكثير من المسائل التي يصعب التعامل معها بالإحداثيات التقليدية، ومن خلال فهم ذلك النظام والتدريب على استخدامه يصب من السهل تحليل أنماط معقدة بطريقة مرنة ودقيقة.