تُعد الفرضيات العلمية حجر الأساس في البحوث الأكاديمية والتطبيقية، فهي تمثل التصور المبدئي الذي يسعى الباحث لاختباره والتحقق من صحته من خلال خطوات علمية منظمة، إن اختبار الفرضية لا يُعد مجرد إجراء تقني، بل هو وسيلة للكشف عن الحقائق وتوسيع المعرفة العلمية، ومن هنا تبرز أهمية معرفة كيف يتم اختبار الفرضية عن طريق، وما هي الأدوات التحليلية والإحصائية التي تُستخدم في ذلك، وكيف يمكن من خلالها تصديق أو نفي الفرضيات بناءً على نتائج البحث.
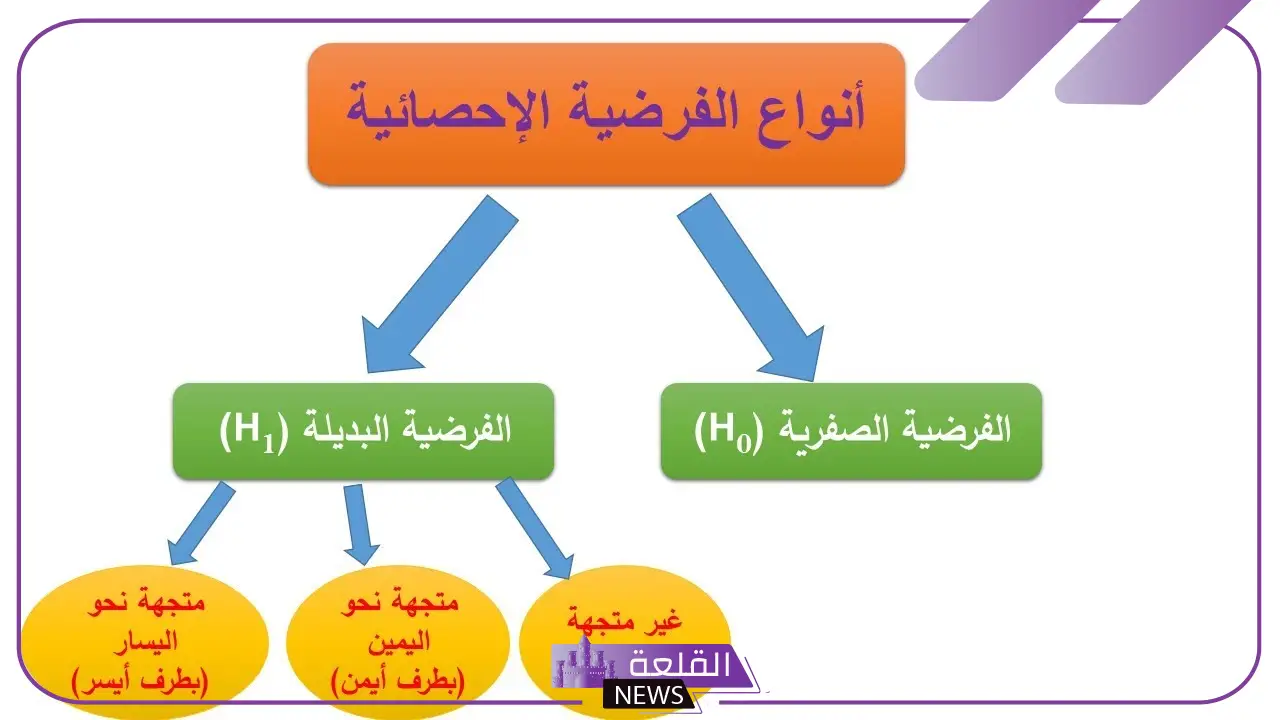
يتم اختبار الفرضية عن طريق
- يتم أولًا تحديد ما إذا كانت الفرضية صفرية (Null Hypothesis) أو بديلة (Alternative Hypothesis)، حيث أن الأولى تنفي وجود علاقة، بينما الثانية تفترض وجودها.
- يجب تصميم أدوات بحث مناسبة لجمع البيانات من عينات تمثل المجتمع الذي تُجرى عليه الدراسة، كاستبيانات أو مقابلات أو ملاحظات.
- يتم تحديد الاختبار الإحصائي بناءً على نوع البيانات ونوع الفرضية، مثل اختبار “ت” أو اختبار “كا²”.
- تُحلل البيانات لمعرفة مدى مطابقتها أو تناقضها مع الفرضية، ويتم احتساب القيمة الاحتمالية (p-value) لتقييم النتائج.
- إذا كانت القيمة الاحتمالية أقل من مستوى الدلالة المعتمد (عادة 0.05)، تُرفض الفرضية الصفرية ويُقبل البديل، والعكس صحيح.
اقرأ أيضًا: تعريف الاحصاء
طرق التحليل
- التحليل الكمي: يعتمد على الأرقام والإحصائيات، ويُستخدم بكثرة في الدراسات التي تهدف إلى قياس الظواهر.
- التحليل النوعي: يركّز على تحليل محتوى النصوص أو الأحاديث أو السلوكيات، ويستخدم في الدراسات الاجتماعية أو السلوكية.
- تحليل المقارنة: يُستخدم عند وجود أكثر من مجموعة أو متغير، ويهدف إلى مقارنة النتائج وتفسير الفروق أو التشابهات بينها.
- تحليل الاتجاهات: يُستخدم لدراسة التغيرات التي تطرأ على المتغيرات عبر الزمن أو الظروف المختلفة.
- التحليل التنبؤي: يُستخدم لتوقّع النتائج المستقبلية بناءً على البيانات السابقة باستخدام نماذج مثل الانحدار الخطي أو تحليل السلاسل الزمنية.
الطرق الإحصائية
- اختبار “ت” (T-test): يُستخدم لمقارنة متوسطات مجموعتين واختبار ما إذا كانت الفروقات بينهما ذات دلالة إحصائية.
- تحليل التباين (ANOVA): يستخدم عندما تكون هناك ثلاث مجموعات أو أكثر ويهدف لمقارنة الفروق بينها.
- اختبار مربع كاي (Chi-Square): يُستخدم لاختبار العلاقة بين متغيرين نوعيين (اسميين أو وصفيين).
- الانحدار الخطي (Linear Regression): يُستخدم لتحليل العلاقة بين متغير تابع وعدة متغيرات مستقلة.
- الارتباط (Correlation): يُستخدم لقياس قوة العلاقة واتجاهها بين متغيرين كميين.
كيف تعمل على تصديق أو نفي الفرضيات وما علاقة ذلك مع نتائج الدراسة
- تحديد مستوى الدلالة: يُحدد مسبقًا مستوى الثقة المقبول (مثل 95%) لتقييم ما إذا كانت النتائج تدعم الفرضية أم لا.
- تحليل القيمة الاحتمالية (p-value): إذا كانت القيمة أقل من مستوى الدلالة، فإننا نرفض الفرضية الصفرية ونصدق البديلة.
- الربط بين النتائج والفرضية: تُقارن نتائج الدراسة بما تنبأت به الفرضية لمعرفة مدى التطابق أو التناقض.
- استخدام التكرار والتجارب الموازية: التأكيد على النتائج من خلال إعادة التجربة أو مقارنة نتائج مشابهة يزيد من إمكانية تصديق الفرضية.
- التفسير العلمي للنتائج: لا يُكتفى برفض أو قبول الفرضية بل يجب تحليل السبب خلف النتائج وربطها بالنظرية أو الإطار المفاهيمي المستخدم.
اقرأ أيضًا: كيف يمكن حساب معاملة الصعوبة
إن يتم اختبار الفرضية عن طريق يُعتبر أحد الركائز الأساسية للبحث العلمي، لأنه يوفر أداة موثوقة لفحص العلاقات بين المتغيرات وفهم الظواهر بدقة، ومن خلال دمج الطرق التحليلية والإحصائية وتفسير النتائج ضمن الإطار البحثي، يمكن الوصول إلى استنتاجات علمية دقيقة تدعم المعرفة وتُسهم في تطوير الفهم العلمي.